การแปลงทางเรขาคณิต
- ความหมายของการแปลงทางเรขาคณิต การแปลงทางเรขาคณิต คือ การจับคู่ของรูปบนระนาบ เป็นการจับคู่ระหว่างจุดบนรูปต้นแบบกับจุดบนรูปที่เกิดจากการแปลงแบบจุดต่อจุด ซึ่งมีผลทำให้รูปที่ได้จากการแปลงมีหลายแบบ บางรูปยังคงลักษณะและความยาวระหว่างจุดเท่าเดิมเช่นเดียวกับรูปต้นแบบการแปลงในลักษณะนี้มี 3 แบบคือการเลื่อนขนาน การสะท้อน และการหมุนดร.สำราญ มีแจ้งและดร.รังสรรค์ มณีเล็ก ( 2547 : 130 )
- การแปลงทางเรขาคณิต คือการย้ายตำแหน่งของรูปเรขาคณิตที่เป็น “รูปต้นแบบ” และรูปที่ได้จากการแปลงเรียกว่า “ ภาพ ” สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยีกระทรวงศึกษาธิการ ( 2546 : 131 )
- การเลื่อนขนานคือ การแปลงที่จับคู่แต่ละจุดของรูปต้นแบบกับจุดแต่ละจุดของรูปที่ได้จากการเลื่อนขนานการเลื่อนขนานจะต้องเลื่อนไปในทิศทางใดทิศทางหนึ่งในระยะทางที่ต้องการ
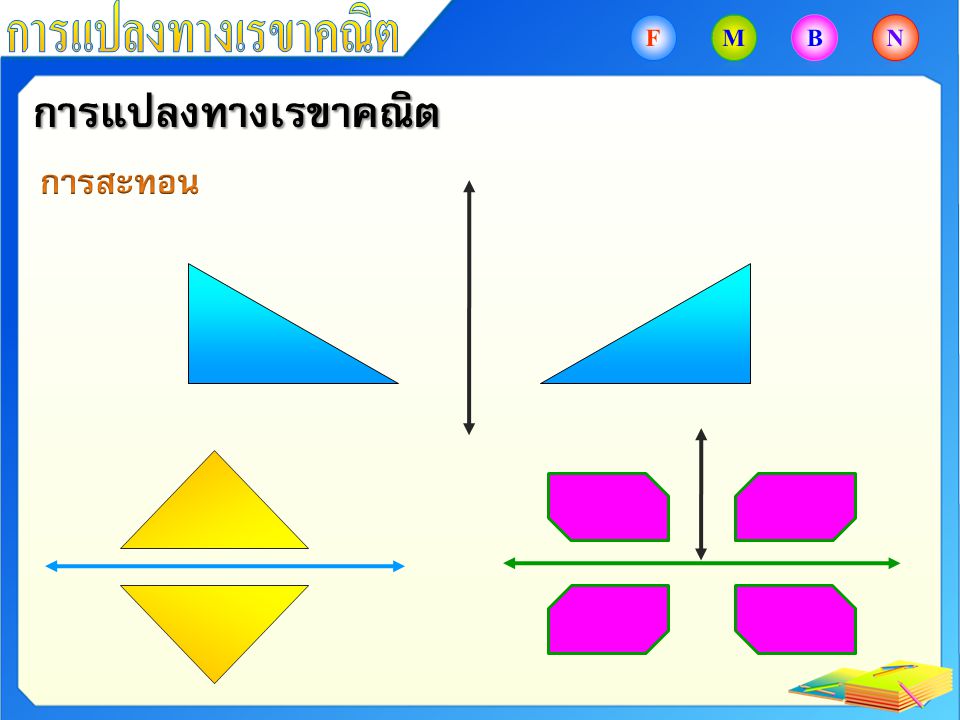
- สมบัติการสะท้อน
- การสะท้อนต้องมีรูปต้นแบบมีเส้นสะท้อนรูปที่เกิดจากการสะท้อนเสมือนการพลิกรูปต้นแบบข้ามเส้นสะท้อนและรูปที่ได้จากการสะท้อนจะมีขนาดและรูปร่างเท่ากับรูปต้นแบบ
- จุดแต่ละจุดบนรูปที่ได้จากการสะท้อนกับจุดบนรูปต้นแบบที่สมนัยกันจะห่างจากเส้น สะท้อนเท่ากันและตั้งฉากกันจุดเหล่านั้นจึงคงที่
- เมื่อดำเนินการสะท้อนจุดบนเส้นของการสะท้อนจะไม่เปลี่ยนแปลงตำแหน่ง
- การหมุน คือ การแปลงที่เกิดจากจับคู่ระหว่างจุดแต่ละจุดบนรูปต้นแบบกับจุดแต่ละจุดบนรูปที่ได้จากการหมุนโดยแต่ละจุดบนรูปต้นแบบเคลื่อนที่รอบจุดหมุนด้วยขนาดของมุมที่กำหนดให้และจุดแต่ละจุดคู่ที่สมนัยกันจะมีระยะห่างจากจุดหมุนเท่ากัน และการหมุนต้องมีจุดหมุนจะอยู่นอกหรือในรูปต้นแบบก็ได้การหมุนจะตามเข็มหรือทวนเข็มนาฬิกาตามขนาด

ไม่มีความคิดเห็น:
แสดงความคิดเห็น